Auto neural networks vs. Manual Keras neural model
June 11, 2018
R modelling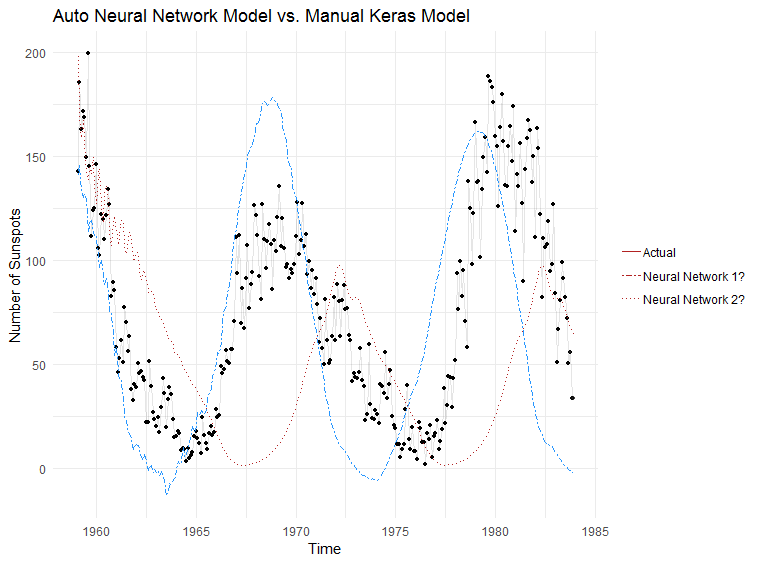
Several posts back I tested two packages for neural network time-series forecasting on the AirPassengers dataset.
I want to now test nnetar against a full neural network framework (Keras) and see how it fares.
Dataset
R contains a dataset called sunspots that is extremely long (starts from 1750s) and exhibits some nice seasonal patterns. This is the training data that we shall use for both models:

And this is the testing data which we will test our models against:

nnetar
We will use the following code to generate a forecast with nnetar:
# Fitting nnetar model
sun.fit.mlp <- nnetar(sun.train)
sun.fcst.mlp <- forecast(sun.fit.mlp, h = 299)(Note that it only takes 2 lines of code to generate this forecast!)
Here are the model details:
## Series: sun.train
## Model: NNAR(25,1,13)[12]
## Call: nnetar(y = sun.train)
##
## Average of 20 networks, each of which is
## a 25-13-1 network with 352 weights
## options were - linear output units
##
## sigma^2 estimated as 119Keras
Setting up Keras to do a similar forecast is much more involved.
Step 1 - we will need to manually prepare the dataset into a format that Keras can understand. The code is a bunch of scaling, centering and turning the data from a tibble/data.frame to a matrix. I will skip showing that section as I suspect you’ll find it boring and it takes up quite a bit of room.
Step 2 - we can now construct a Keras model:
# Model params
units <- 256
inputs <- 1
# Create model
model.keras <- keras_model_sequential()
model.keras %>%
layer_dense(units = units,
input_shape = c(lookback),
batch_size = inputs,
activation = "relu") %>%
layer_dense(units = units/2,
activation = "relu") %>%
layer_dense(units = units/8,
activation = "relu") %>%
layer_dense(units = 1)
# Compile model
model.keras %>% compile(optimizer = "rmsprop",
loss = "mean_squared_error",
metrics = "accuracy")Step 3 - we can now attempt to train the model:
## Model
## ___________________________________________________________________________
## Layer (type) Output Shape Param #
## ===========================================================================
## dense_1 (Dense) (1, 256) 37120
## ___________________________________________________________________________
## dense_2 (Dense) (1, 128) 32896
## ___________________________________________________________________________
## dense_3 (Dense) (1, 32) 4128
## ___________________________________________________________________________
## dense_4 (Dense) (1, 1) 33
## ===========================================================================
## Total params: 74,177
## Trainable params: 74,177
## Non-trainable params: 0
## ___________________________________________________________________________Step 4 - we can now make predictions from the model:
## Predict based on last observed sunspot number
n <- 299 #number of predictions to make
predictions <- numeric() #vector to hold predictions
# Generate predictions, starting with last observed sunspot number and feeding
# new predictions back into itself
for(i in 1:n){
pred.y <- x[(nrow(x) - inputs + 1):nrow(x), 1:lookback]
dim(pred.y) <- c(inputs, lookback)
# forecast
fcst.y <- model.keras %>% predict(pred.y, batch_size = inputs)
fcst.y <- as_tibble(fcst.y)
names(fcst.y) <- "x"
# Add to previous dataset sun.tibble.rec
sun.tibble.rec <- rbind(sun.tibble.rec, fcst.y)
## Recalc lag matrix
# Setup a lagged matrix (using helper function from nnfor)
sun.tibble.rec.lag <- nnfor::lagmatrix(sun.tibble.rec$x, 0:lookback)
colnames(sun.tibble.rec.lag) <- paste0("x-", 0:lookback)
sun.tibble.rec.lag <- as_tibble(sun.tibble.rec.lag) %>%
filter(!is.na(.[, ncol(.)])) %>%
as.matrix()
# x is input (lag), y is output, multiple inputs
x <- sun.tibble.rec.lag[, 2:(lookback + 1)]
dim(x) <- c(nrow(x), ncol(x))
y <- sun.tibble.rec.lag[, 1]
dim(y) <- length(y)
# Invert recipes
fcst.y <- fcst.y * (range.max.step - range.min.step) + range.min.step
# save prediction
predictions[i] <- fcst.y %>%
InvBoxCox(l)
predictions <- unlist(predictions)
}Results!
And the moment we have been waiting for… which model does a better job at making predictions?
Conclusion
Total number of lines of code to generate a forecast with nnetar: 2
Total number of lines of code to generate a forecast with Keras: 116
I’ll let you decide which one is worth it. I’ll likely run it through nnetar and depending on the results then decide if it’s worth going down the manual route. If nothing else, nnetar provides a nice baseline forecast to compare with.